Someone recently asked me, “What is something surprising or amusing you learned recently?” I solved a puzzle that is counterintuitive on its face but makes total sense after thinking it through.
So, since I started driving recently, I noticed that if back-to-back cars have equal acceleration, they naturally create a following distance based on the following driver’s reaction time. Is this real? Kinematics and integrals to the rescue!
So, first, let’s pretend that we have two cars with following distance \(d_f = 0\) at a traffic light. At t=0, the lights turn green, and the velocity of both cars is 0. Velocity-time graphs are the key here because they show both distance and acceleration as area and slope, respectively.

At t=1 the front car starts accelerating at a constant acceleraiton of \(1m/s^2\), and at t=2, trying to match the front car, the back car does the same.
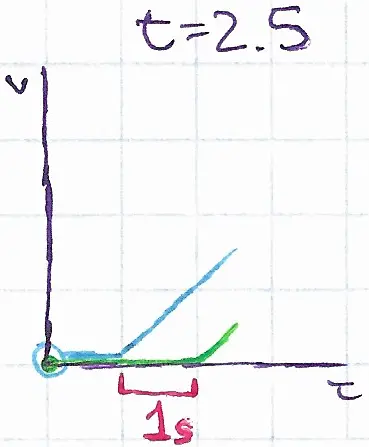
Then, let’s say, at t=4, at 3m/s, the front stops accelerating, and at t=5, after reaching the same velocity, the back stops accelerating.
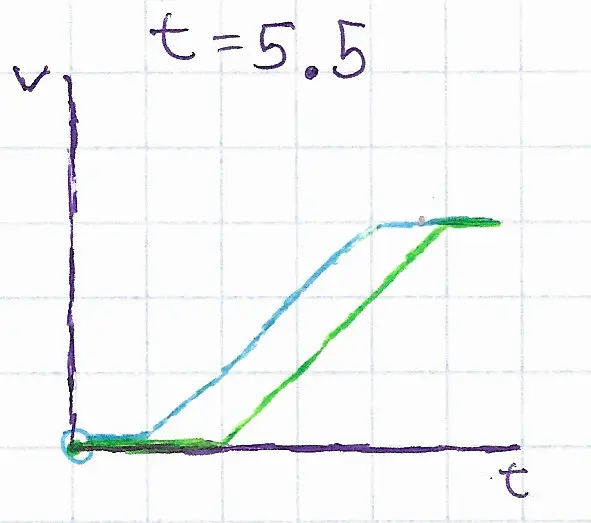
Throughout the period when they were both accelerating, they had a velocity differential relative to one another of 1m/s. That is where they gain the following distance. Since acceleration is constant, but velocity is not equal.
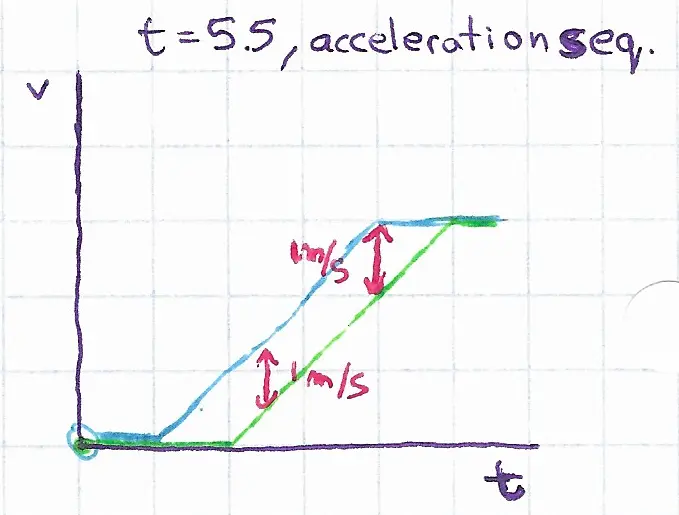
The area between those two curves, \(d_f = \int v_b - v_g \, dt\) is the following distance, the parallelogram, in this case, is equal to the total velocity times the reaction time, \(3m/s * 1s = 3m\).
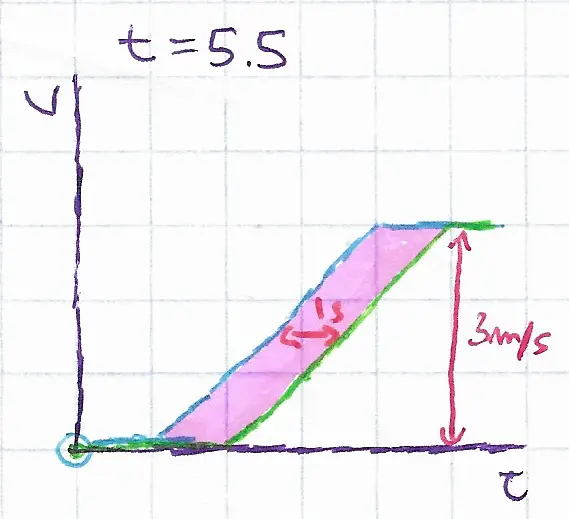
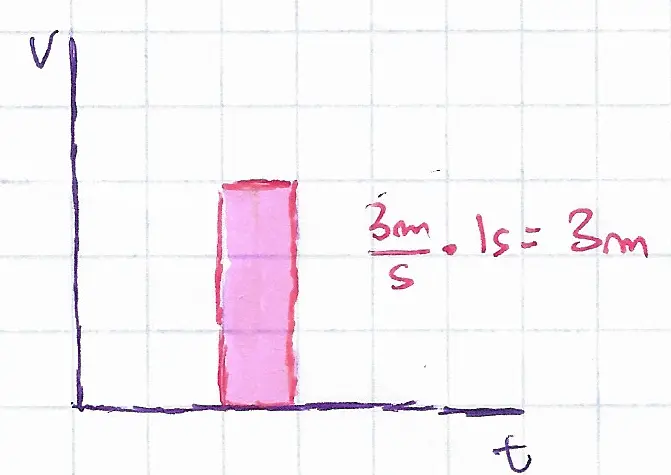
The same phenomenon applies when braking, where as two drivers push on the break equally hard, the distance between them gradually decreases as they come to a stop.
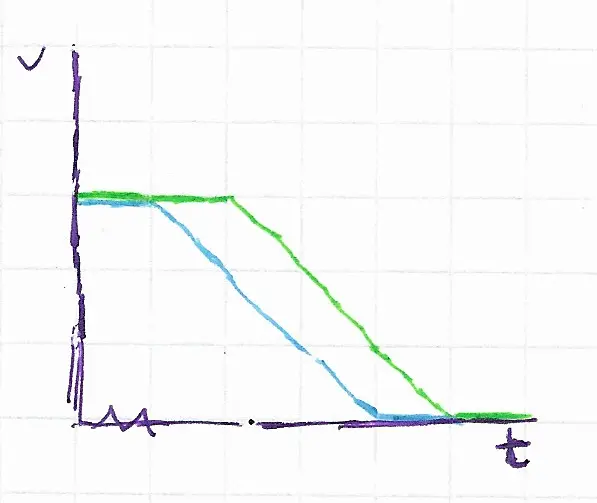
Looking at the distance-time graph, which starts quadratic and then settles into linear, explains this phenomenon even better.
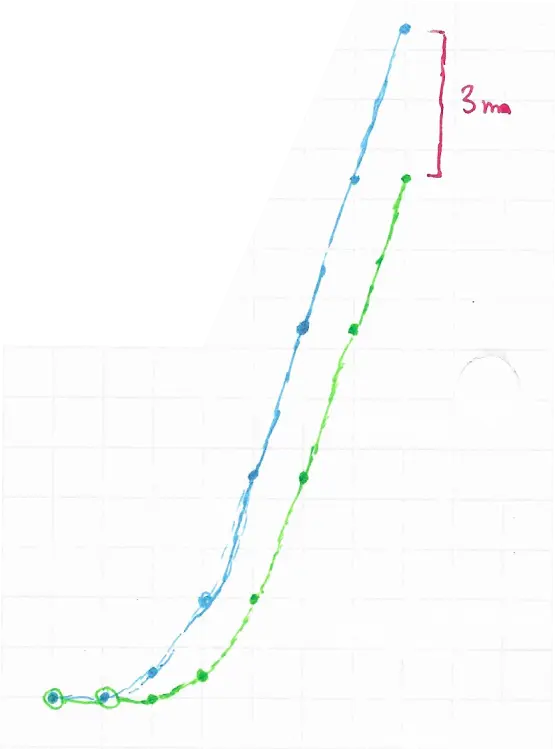
P.S. Humans do not drive with constant acceleration and instead have complex feedback loops. This is simply a high-level overview of this pattern in an ideal universe.
Comments